Mohamed Talhaoui

Tri par Sélection (Selection Sort)

C :

void selectionSort(int arr[], int n) {
    int i, j, min_idx;
    for (i = 0; i < n-1; i++) {
        min_idx = i;
        for (j = i+1; j < n; j++)
            if (arr[j] < arr[min_idx])
                min_idx = j;
        int temp = arr[min_idx];
        arr[min_idx] = arr[i];
        arr[i] = temp;
    }
}

Visualisation du Tri par Sélection

Tri par Insertion (Insertion Sort)

C :

void insertionSort(int arr[], int n) {
    int i, key, j;
    for (i = 1; i < n; i++) {
        key = arr[i];
        j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

Visualisation du Tri par Insertion

Tri à Bulles (Bubble Sort)

C :

void triBulle(int T[], int taille)
{
    for (int i = 0 ; i < taille - 1 ; i++)
    {
        for (int j = 0; j < taille - i - 1; j++)
        {
            if (T[j] > T[j + 1])
            {
                echanger(&T[j], &T[j + 1]);
            }
        }
    }

}

void echanger(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

Visualisation du Tri à Bulles

Tri Fusion (Merge Sort)

C :

void triFusion(int T[], int g, int d)
{
    if (g < d)
    {
        int m = (g + d) / 2;
        triFusion(T, g, m);
        triFusion(T, m + 1, d);
        fusion(T, g, m, d);
    }
}

void fusion(int T[], int g, int m, int d)
{
    int i, j, k;
    int n1 = m - g + 1;
    int n2 = d - m;
    int Tg[n1], Td[n2];
    for (i = 0; i < n1; i++)
    {
        Tg[i] = T[g + i];
    }
    for (j = 0; j < n2; j++)
    {
        Td[j] = T[m + 1 + j];
    }
    i = 0;
    j = 0;
    k = g;
    while (i < n1 && j < n2) 
    {
        if (Tg[i] <= Td[j]){
            T[k] = Tg[i];
            i++;
        }
        else {
            T[k] = Td[j];
            j++;
        }
        k++;
    }
    while (i < n1)
    {
        T[k] = Tg[i];
        i++;
        k++;
    }
    while (j < n2)
    {
        T[k] = Td[j];
        j++;
        k++;
    }
}

Visualisation du Tri Fusion

Tri Rapide (Quick Sort)

C :
                
void triRapide(int T[], int bas, int haut)
{
    if (bas < haut)
    {
        int pi = partition(T, bas, haut);
        triRapide(T, bas, pi - 1);
        triRapide(T, pi + 1, haut);
    }
}
int partition(int T[], int bas, int haut)
{
    int pivot = T[haut];
    int i = (bas - 1);
    for (int j = bas; j < haut; j++)
    {
        if (T[j] <= pivot)
        {
            i++;
            echanger(&T[i], &T[j]);
        }
    }
    echanger(&T[i + 1], &T[haut]);
    return (i + 1);
}

void echanger(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

Visualisation du Tri Rapide

Tri Par Tas (Heap Sort)

C :
                                
void triTas(int T[], int taille)
{
    for (int i = taille / 2 - 1 ; i >= 0 ; i--)
    {
        tas(T, taille, i);
    }
    for (int i = taille - 1 ; i >= 0 ; i--)
    {
        echanger(&T[0], &T[i]);
        tas(T, i, 0);
    }
}

void tas(int T[], int taille, int i)
{
    int maxIdx = i;
    int g = 2 * i + 1;
    int d = 2 * i + 2;
    if (g < taille && T[g] > T[maxIdx])
    {
        maxIdx = g;
    }
    if (d < taille && T[g] > T[maxIdx]) 
    {
        maxIdx = d;
    }
    if (maxIdx != i)
    {
        echanger(&T[i], &T[maxIdx]);
        tas(T, taille, maxIdx);
    }
}

void echanger(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

Visualisation du Tri Par Tas

Recherche Séquentielle (Linear Search)

C :

int linearSearch(int arr[], int n, int target) {
    for (int i = 0; i < n; i++)
        if (arr[i] == target)
            return i;
    return -1;
}

Visualisation de la Recherche Séquentielle

Recherche Dichotomique (Binary Search)

C :

int binarySearch(int arr[], int l, int r, int target) {
    while (l <= r) {
        int m = l + (r - l) / 2;
        if (arr[m] == target)
            return m;
        if (arr[m] < target)
            l = m + 1;
        else
            r = m - 1;
    }
    return -1;
}

Visualisation de la Recherche Dichotomique

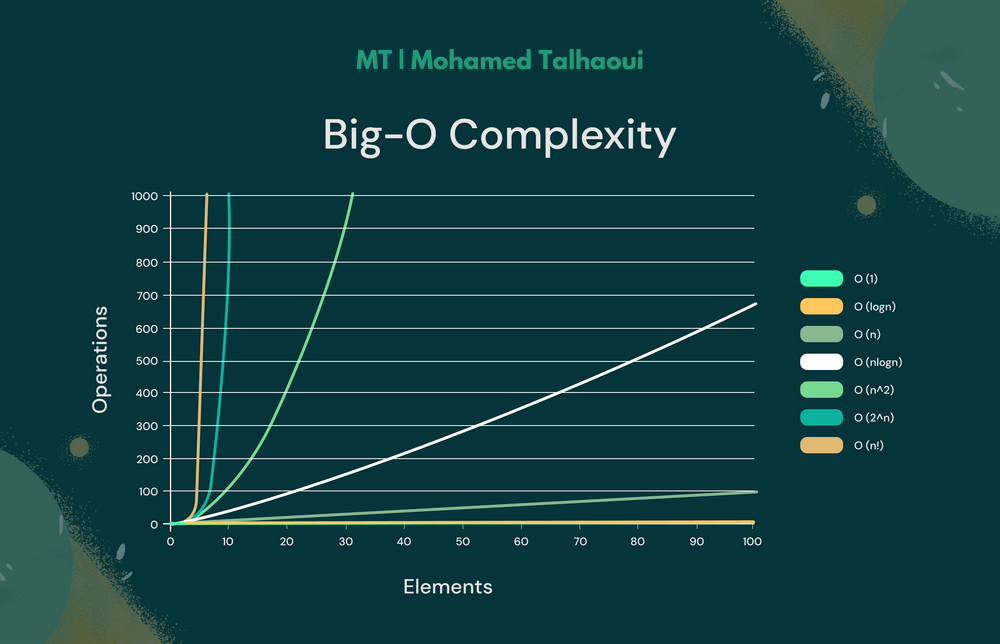
Notation Big O

Définition : Décrit la borne supérieure du temps d'exécution d'un algorithme. Elle donne le pire des cas de la manière dont le temps d'exécution augmente avec la taille de l'entrée.

Classes courantes :

• O(1) : Temps constant.
• O(log n) : Temps logarithmique.
• O(n) : Temps linéaire.
• O(n log n) : Temps linéarithmique.
• O(n²) : Temps quadratique.
• O(2ⁿ) : Temps exponentiel.
• O(n!) : Temps factoriel.

Complexité Temporelle

Définition : Mesure la quantité de temps qu'un algorithme prend pour s'exécuter en fonction de la longueur de l'entrée.

Classes courantes :

• P : Problèmes résolubles en temps polynomial.
• NP : Problèmes pour lesquels une solution donnée peut être vérifiée en temps polynomial.
• NP-difficile : Problèmes aussi difficiles que les problèmes les plus difficiles de NP ; pas nécessairement dans NP.
• NP-complet : Problèmes de NP qui sont NP-difficiles.

Complexité Spatiale

Définition : Mesure la quantité de mémoire qu'un algorithme utilise en fonction de la longueur de l'entrée.

Classes courantes :

• PSPACE : Problèmes résolubles en utilisant une quantité polynomiale d'espace.
• L : Problèmes résolubles en espace logarithmique.
• NL : Problèmes résolubles en espace logarithmique non déterministe.

Analyse de la Complexité

Cas moyen : Représente la complexité dans la plupart des situations.

Pire cas : La complexité la plus élevée, souvent analysée avec la notation Big-O.

Meilleur cas : La complexité minimale, mais rarement utilisée pour évaluer les performances globales.

Importance de la Complexité

Optimisation : La complexité aide à choisir l'algorithme le plus performant pour un problème donné, en fonction des ressources disponibles (temps et mémoire).

Scalabilité : Une bonne analyse de la complexité permet de savoir si un algorithme peut gérer de grandes tailles d'entrées de manière efficace.

Techniques pour Réduire la Complexité

Diviser pour régner : Diviser un problème en sous-problèmes plus petits, comme dans les algorithmes de tri (ex. tri rapide, tri fusion).

Approximations : Pour les problèmes NP-complets, utiliser des algorithmes d'approximation ou des heuristiques.

Mémoïsation et programmation dynamique : Stocker les résultats intermédiaires pour éviter les calculs redondants.

Listes

Une liste est une collection ordonnée d'éléments.

Piles

Une pile est une structure de données LIFO (Last In, First Out).

Files

Une file est une structure de données FIFO (First In, First Out).